Scaling llama.cpp on Neoverse N2: Solving Cross-NUMA Performance Issues

This blog post explains the cross-NUMA memory access issue that occurs when you run llama.cpp in Neoverse. It also introduces a proof-of-concept patch that addresses this issue and can provide up to a 55% performance increase for text generation when you run the llama3_Q4_0 model on the ZhuFeng Neoverse system.

Cross-NUMA memory access problem

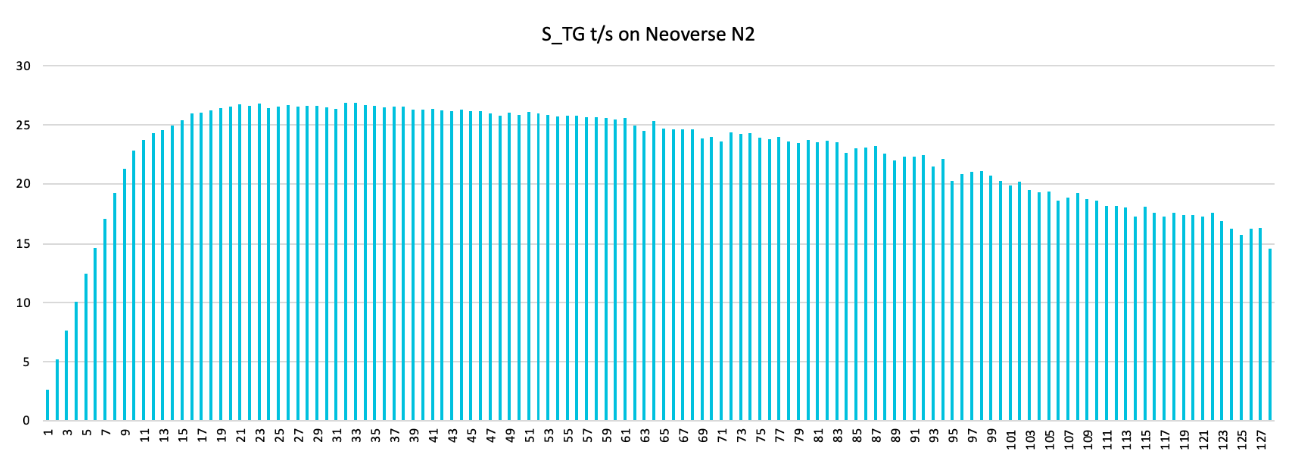
In llama.cpp, performance drops when the number of threads exceeds the number of cores in a NUMA node. This example uses a 64 cores per NUMA node, and the llama3-Q4_0 model.

Root causes

There are two causes for the problem if threads spawn across NUMA nodes:

• The atomic operations in ggml_barrier() across NUMA node is time-consuming.
• Lots of cross NUMA memory access of the tensor buffer of Mul Mat operation.

ggml_barrier issue

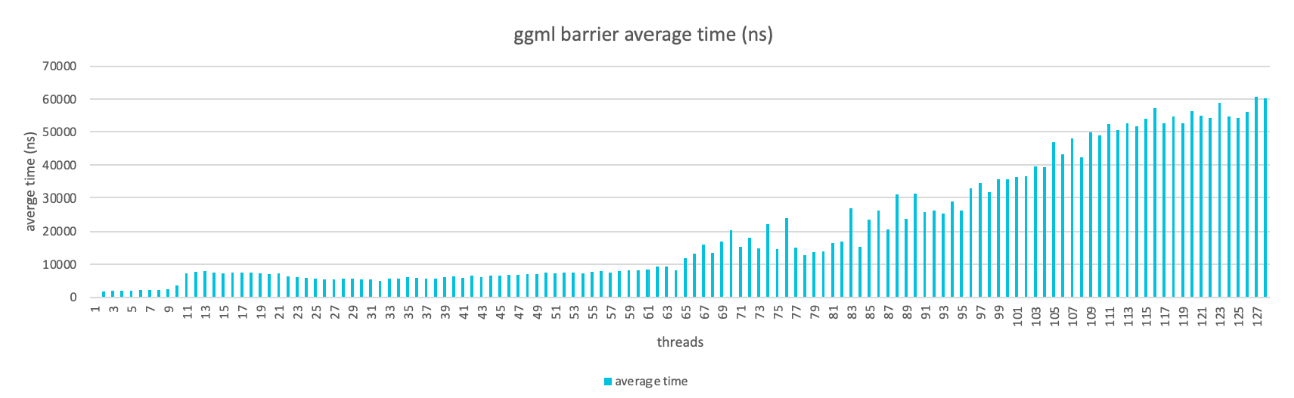
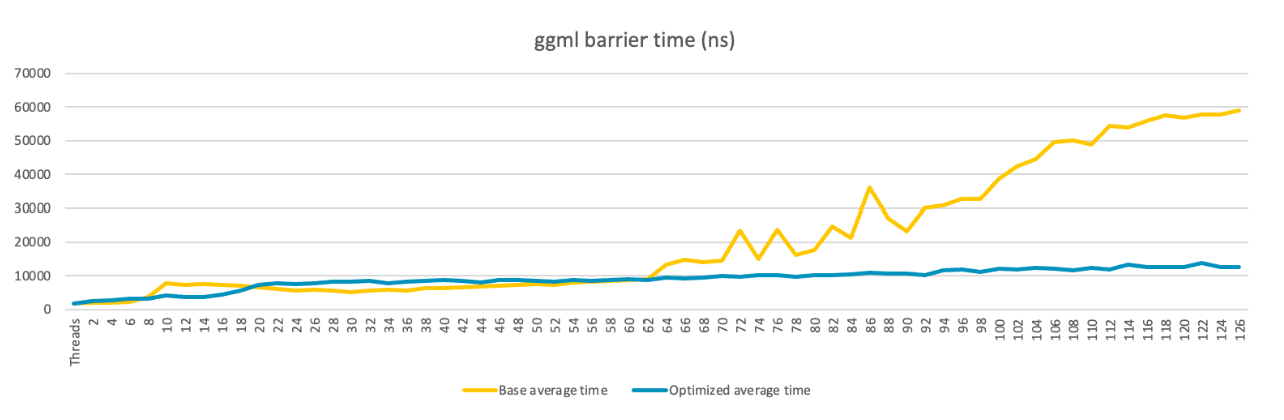
When running llama.cpp in multi-threads, each thread computes part of the tensor data. A barrier is used after all threads finish computation to make sure the data is synced. Performance drops as the number of threads increases and the impact is worse when thread count exceeds a NUMA node (64 cores per node).

Mul Mat operation issue

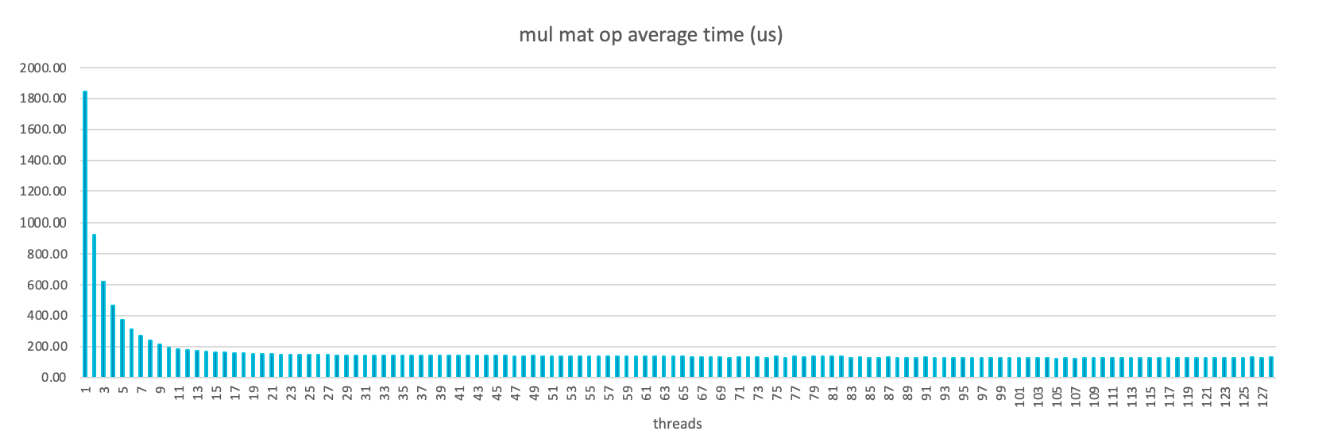
The Mul Mat operation in llama.cpp is the main performance hotspot. In theory, performance should improve as you add more threads. However, this is not the case because the tensor buffer is allocated from malloc() which is not NUMA-aware, and leads to significant cross-NUMA memory access.

Optimization methods

To mitigate the cross NUMA problem in this case, two optimization methods are applied:

1. ggml_barrier optimization
2. Mul Mat operation optimization

ggml_barrier optimization

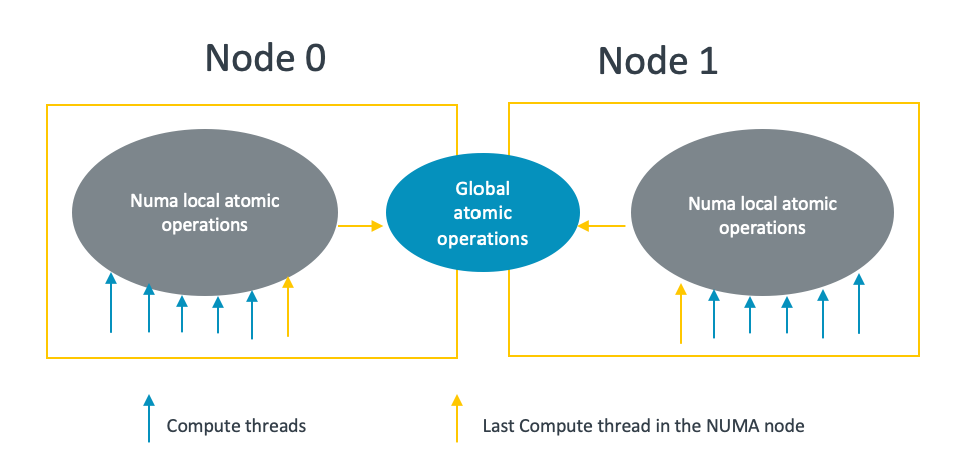
This solution optimizes the ggml barrier by using the ”divide-and-conquer” approach:

• It uses the NUMA local atomic variable to do the barrier which is fast.
• Only the last thread of a specified NUMA node syncs with the last threads of other NUMA nodes in a cross-NUMA way.

With this method, the number of threads performing cross-NUMA global atomic operations is reduced to the number of NUMA nodes involved:

With the optimized ggml barrier, there is no obvious performance drop even if there are cross NUMA operations:

Mul Mat operation optimization

The Mul Mat operation computation uses three tensor buffers: dst (for example, attn_out, ffn_gate, ffn_out, ffn_up, Kcur, Qcur, Vcur, FP32), src0 (weight), and src1 (for example, attn_norm, ffn_gate_par, ffn_norm, kqv_out FP32).

These buffers are allocated using malloc which is not NUMA aware. As a result, many NUMA memory accesses occur when threads exceed a single NUMA node.

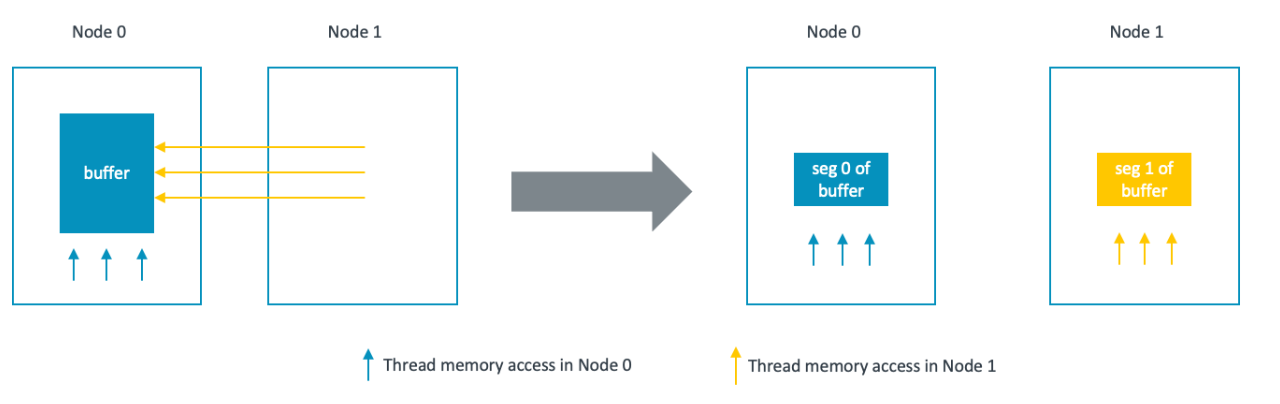
The optimization splits the buffers into segments so that computation threads access memory from their local NUMA node whenever possible.

For dst and src0 buffers, each thread accesses a portion of the buffers based on the thread ID. By splitting the buffer into N segments, where N is the number of NUMA nodes, each thread can access the portion of buffers in its local NUMA node if:

• Thread id is well mapped to the physical core id, which could be set through affinity.
• The segments are moved to the desired NUMA nodes, which could be done through move_pages() system call.

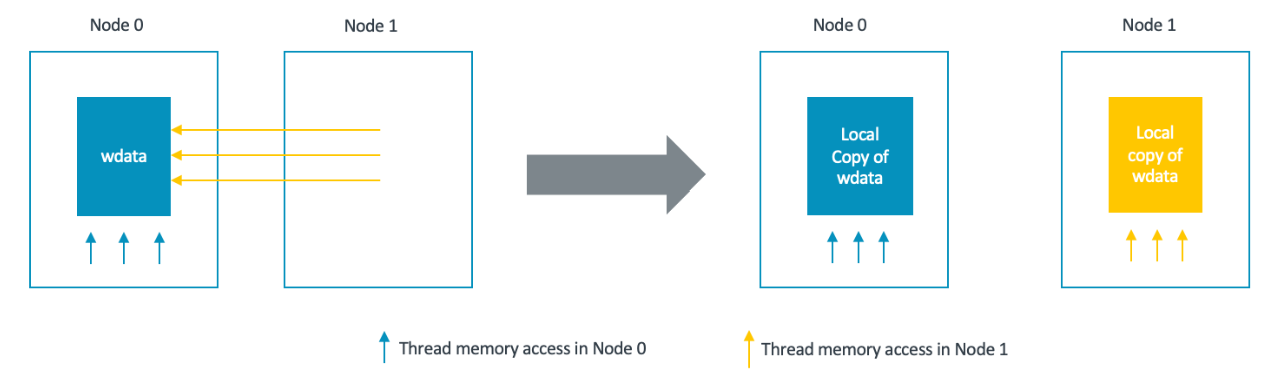
During the Mul Mat operation computation, src1 is quantized and stored in another buffer called wdata. The Mul Mat operation is then computed as:

dst = src0 * wdata

When src0 and dst is accessed by each threads according to thread id, wdata is a buffer which needs to be accessed entirely by those threads.

The approach is based on the fact that quantization is not the main hotspot in the mul_mat operation. A NUMA-local wdata buffer is created for each NUMA node, and all threads in a NUMA node quantize src1 into its own wdata. As a result, there are N copies of wdata.

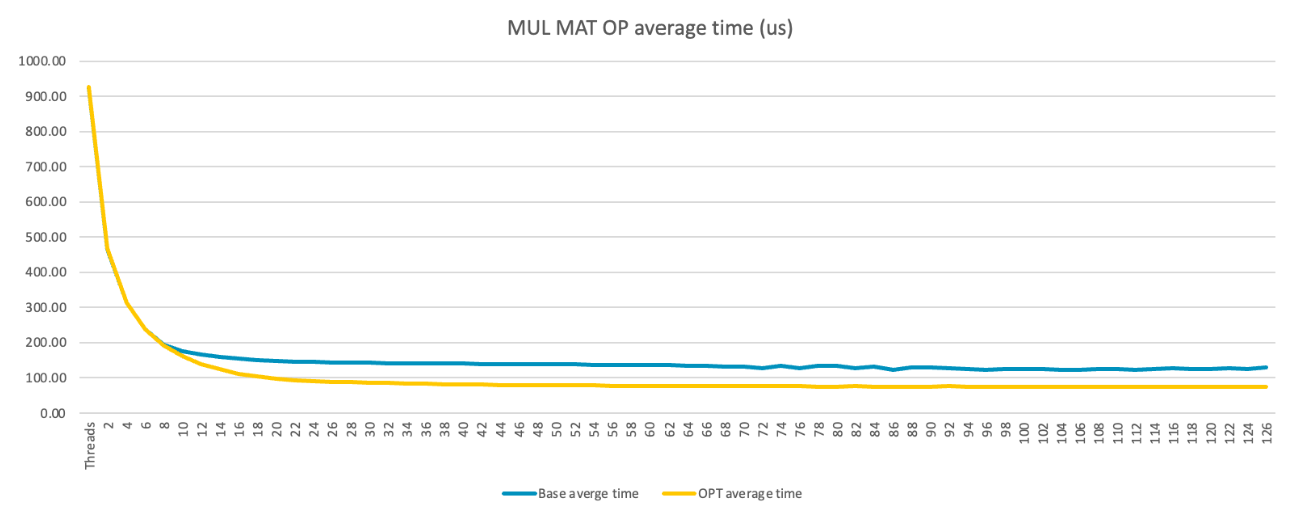
With the optimized tensor data layout for the Mul Mat operation computation, we can see there is a clear performance uplift:

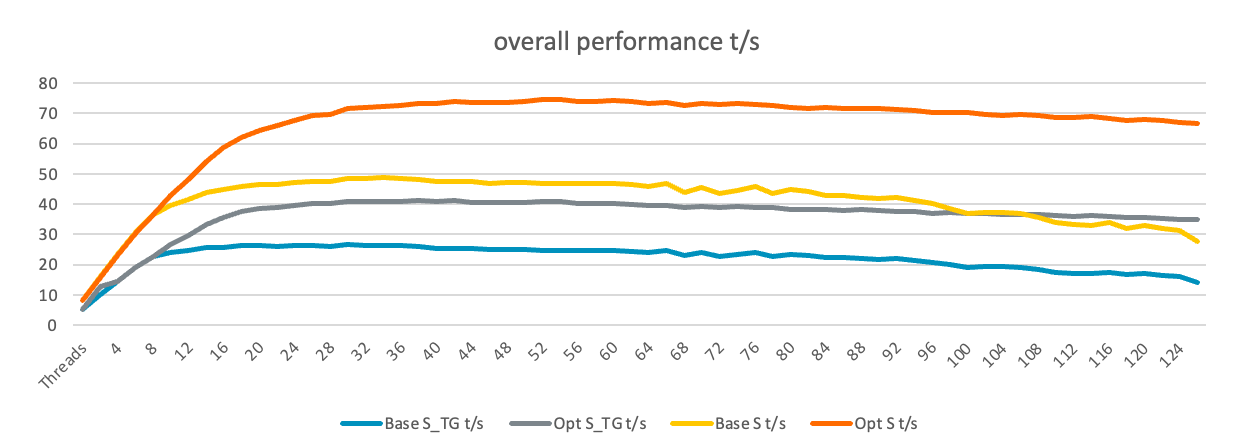
Overall performance comparison

We tested the llama.cpp batched benchmark and the results are:

• With the NUMA optimization there is a clear performance uplift.
• For S_TG t/s, the best number of base is 26.52 with 32 threads. It is 41.15 with 40 threads for the NUMA optimization, which is a 55% uplift.
• For S t/s, the best number of base is 48.73 with 36 threads. It is 74.67 with 54 threads for the NUMA optimization, which is a 53.2% uplift.

By capturing the memory bandwidth data of the NUMA optimization, we see the bandwidth balanced across NUMA nodes. Without the optimization, the bottleneck appears in NUMA node 0. This example uses a two-NUMA-node system:

Use Cases	node 0 bandwidth GB/s	node 1 bandwidth GB/s
Stream test on numa node 0 with 64 threads	119.8	0
llama.cpp numa node 0 with 64 threads	104.9	0
llama.cpp numa node 0 and 1 with 128 threads	70.6	0.2
optimized llama.cpp numa node 0 and 1 with 128 threads	74.4	72.2
optimized llama.cpp numa node 0 and 1 with 54 threads	97.4	99.4

Proof of concept patch

The proof-of-concept NUMA optimization patch was reviewed by a llama.cpp author, but was not merged as interest in server and cloud use cases is low:

NUMA optimization patch on GitHub